Công thức tính bán kính hình tròn trong hình học cơ bản

Hiểu biết cơ bản về hình tròn

Hình tròn là một trong những hình dạng cơ bản nhất trong hình học. Nó được xác định bởi tập hợp các điểm nằm cách đều một điểm trung tâm một khoảng nhất định. Khoảng cách này chính là bán kính của hình tròn. Việc tính toán bán kính của hình tròn rất quan trọng trong nhiều lĩnh vực, từ kiến thức cơ bản trong toán học cho đến ứng dụng thực tế trong kỹ thuật, kiến trúc, và nhiều ngành khác. Hình tròn cũng có nhiều yếu tố liên quan, như đường kính, chu vi, và diện tích. Đường kính là khoảng cách từ một điểm trên vòng tròn này sang một điểm đối diện, chia hình tròn thành hai phần bằng nhau. Trong khi đó, chu vi là độ dài của đường tròn, và diện tích là không gian được bao bọc bởi hình tròn đó.

Công thức tính bán kính từ chu vi và đường kính

Một trong những cách phổ biến để tính bán kính là sử dụng chu vi của hình tròn. Công thức tính chu vi của hình tròn được thể hiện như sau: \[ C = 2\pi r \] Trong đó:

• \(C\) là chu vi
• \(r\) là bán kính
• \(\pi\) là hằng số (khoảng 3.14)

Từ công thức trên, bạn có thể dễ dàng tính bán kính bằng cách chuyển đổi nó: \[ r = \frac{C}{2\pi} \] Nếu bạn biết đường kính của hình tròn, bạn có thể tính bán kính bằng cách đơn giản là chia đường kính cho 2. Công thức này được thể hiện dưới đây: \[ d = 2r \Rightarrow r = \frac{d}{2} \] Trong đó:

• \(d\) là đường kính của hình tròn.

Ví dụ, nếu một hình tròn có đường kính là 10 cm, bán kính sẽ được tính như sau: \[ r = \frac{10}{2} = 5 \text{ cm} \]

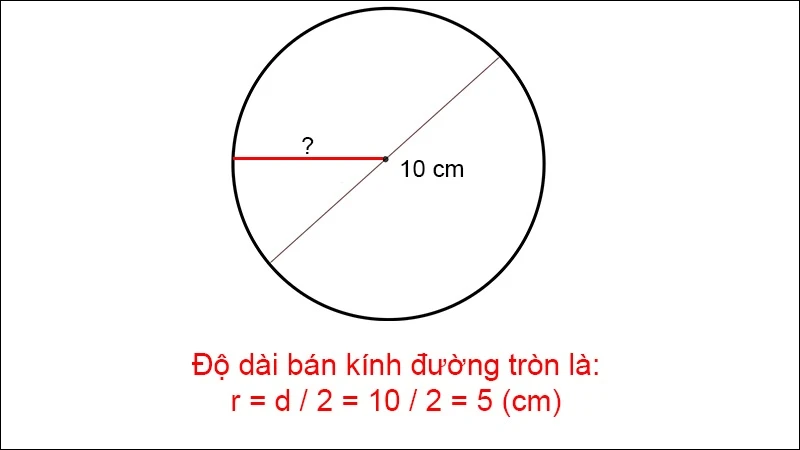
Công thức tính bán kính từ diện tích

Ngoài việc tính bán kính từ chu vi hoặc đường kính, bạn cũng có thể tính bán kính khi biết diện tích của hình tròn. Công thức tính diện tích hình tròn được biểu diễn như sau: \[ S = \pi r^2 \] Trong đó:

• \(S\) là diện tích
• \(r\) là bán kính

Để tính bán kính từ diện tích, bạn cần giải phương trình này như sau: \[ r = \sqrt{\frac{S}{\pi}} \] Chẳng hạn, nếu bạn biết diện tích của một hình tròn là 78.5 cm², bạn có thể tính bán kính như sau: \[ r = \sqrt{\frac{78.5}{\pi}} \approx \sqrt{25} = 5 \text{ cm} \]

Ứng dụng trong thực tế

Bán kính có vai trò quan trọng trong nhiều lĩnh vực khác nhau. Ví dụ, trong ngành xây dựng, việc tính toán bán kính giúp các kỹ sư thiết kế các công trình như cầu, đường, và các kiến trúc hình tròn khác. Trong lĩnh vực vật lý, bán kính thường được sử dụng trong các tính toán liên quan đến chuyển động của các đối tượng trong không gian. Trong giáo dục, việc hiểu và nắm vững các công thức tính bán kính sẽ giúp học sinh dễ dàng hơn trong việc giải quyết các bài toán hình học phức tạp hơn. Bên cạnh đó, việc áp dụng các công thức này trong thực tế cũng giúp nâng cao khả năng tư duy logic và phân tích.

Kết luận

Như vậy, việc tính bán kính là một phần quan trọng trong toán học và có nhiều ứng dụng thực tiễn. Từ các công thức đơn giản về chu vi, diện tích cho đến đường kính, người học có thể dễ dàng vận dụng các kiến thức này vào thực tiễn. Hãy nhớ rằng việc nắm vững các công thức và phương pháp tính toán không chỉ giúp bạn trong học tập mà còn cả trong cuộc sống hàng ngày. Các công thức này không chỉ là lý thuyết mà còn là kiến thức thực tiễn, giúp bạn giải quyết bài toán một cách nhanh chóng và chính xác. Hãy thường xuyên luyện tập và áp dụng để trở thành một người thành thạo trong việc tính toán các yếu tố liên quan đến hình tròn!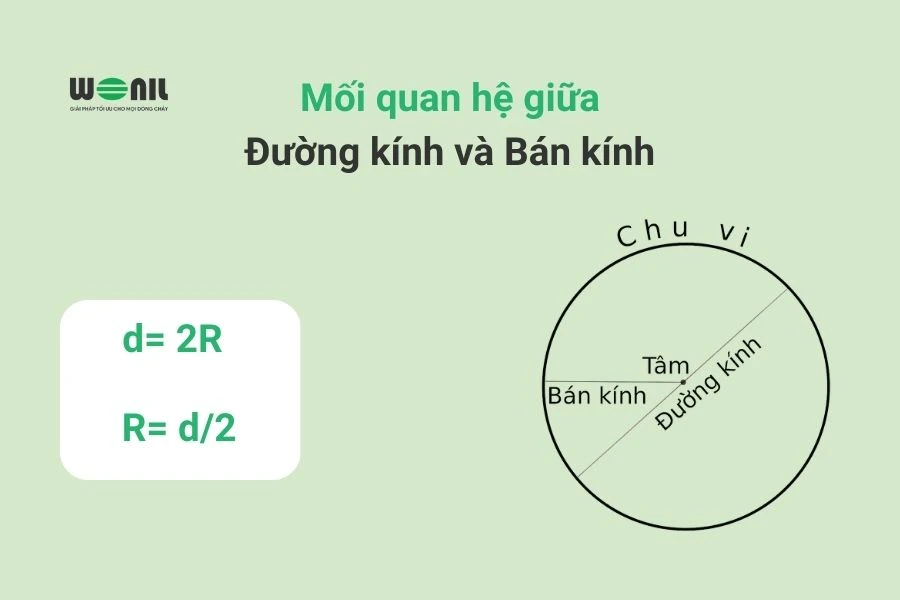

Một số bài tập thực hành

Để củng cố kiến thức, bạn có thể thử giải một số bài tập thực hành sau:

• Tính bán kính của hình tròn có chu vi là 31.4 cm.
• Tìm bán kính khi diện tích hình tròn là 50 cm².
• Nếu một hình tròn có đường kính là 12 cm, hãy tính chu vi và diện tích của nó.

Hãy thực hành và kiểm tra kết quả của bạn để củng cố hiểu biết về bán kính và các công thức liên quan.