Công thức tính thể tích của hình trụ trong toán học

Khám Phá Hình Trụ: Từ Cấu Tạo Đến Công Thức Tính Toán

Trong toán học, có rất nhiều hình dạng khác nhau, mỗi hình đều có những đặc điểm và ứng dụng riêng. Trong số đó, hình trụ là một trong những hình dạng phổ biến và thú vị. Bài viết này sẽ khám phá hình trụ, cách tính thể tích của nó cũng như ứng dụng của công thức này trong thực tế.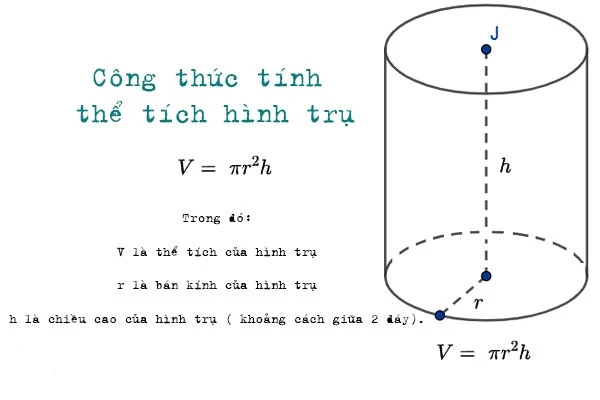

1. Hình Trụ Là Gì?

Định Nghĩa

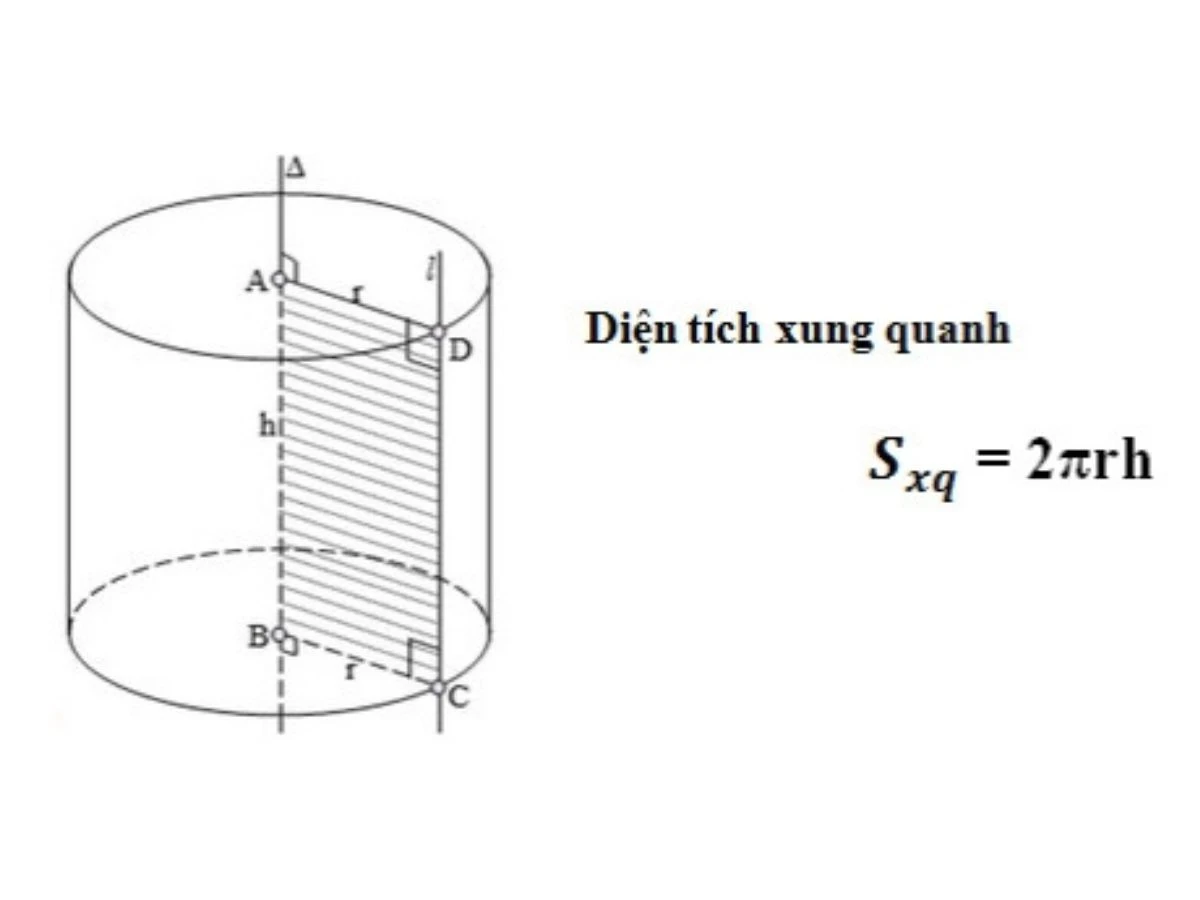
Hình trụ là một khối hình học ba chiều, được tạo thành từ hai mặt đáy có hình tròn và một bề mặt xung quanh thẳng đứng nối liền hai mặt đáy đó. Hình trụ thường được mô tả bằng các thông số như bán kính đáy và chiều cao.

Các Thành Phần Của Hình Trụ

• Bán kính (r): Là khoảng cách từ tâm của đáy đến bất kỳ điểm nào trên viền đáy.
• Chiều cao (h): Là khoảng cách giữa hai mặt đáy của hình trụ, đo theo phương thẳng đứng.
• Mặt đáy: Là hai hình tròn dẹt nằm ở hai đầu của hình trụ.

Những khái niệm này giúp chúng ta hiểu rõ hơn về hình trụ và cách thức mà nó hoạt động trong không gian ba chiều.

2. Tính Thể Tích Của Hình Trụ

Công Thức Tính Thể Tích

Để tính thể tích của hình trụ, chúng ta sử dụng công thức đơn giản sau: \[ V = \pi r^2 h \] Trong đó:

• \( V \) là thể tích của hình trụ.
• \( r \) là bán kính đáy.
• \( h \) là chiều cao.
• \( \pi \) (pi) là một hằng số toán học, xấp xỉ bằng 3.14159.

Công thức trên cho phép chúng ta tính được thể tích của hình trụ chỉ bằng cách biết bán kính đáy và chiều cao của nó.

Giải Thích Công Thức

Công thức này có thể được hiểu như sau:

• \( \pi r^2 \): Đây là diện tích của mặt đáy hình trụ. Mặt đáy là một hình tròn, và diện tích hình tròn được tính bằng công thức \( \pi r^2 \).
• \( h \): Chiều cao của hình trụ. Khi nhân diện tích đáy với chiều cao, chúng ta sẽ có thể tích của hình trụ, tức là số không gian mà hình trụ chiếm trong không gian ba chiều.

Ví Dụ Minh Họa

Giả sử bạn có một hình trụ với bán kính đáy là 3 cm và chiều cao là 5 cm. Để tính thể tích của hình trụ, chúng ta sẽ thay các giá trị vào công thức: \[ V = \pi (3)^2 (5) = \pi \times 9 \times 5 = 45\pi \] Khi tính toán giá trị cụ thể, \( 45\pi \) xấp xỉ bằng 141.37 cm³.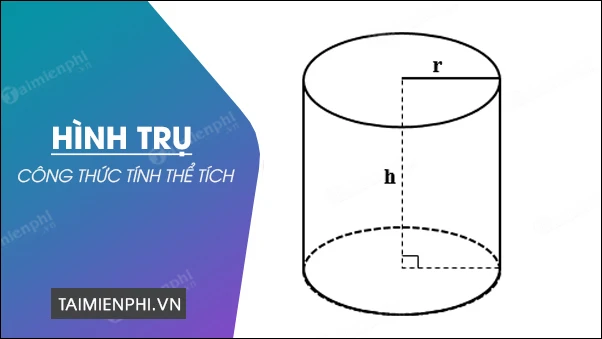

3. Ứng Dụng Của Công Thức Tính Thể Tích Hình Trụ

Trong Đời Sống Hàng Ngày

Công thức tính thể tích của hình trụ có nhiều ứng dụng thực tế. Một số ví dụ cụ thể bao gồm:

• Chứa đựng chất lỏng: Các thùng nước, can nhựa hay chai nhựa đều có hình dạng giống hình trụ. Biết được thể tích của chúng giúp chúng ta biết được chúng có thể chứa bao nhiêu chất lỏng.
• Kiến trúc: Trong xây dựng, các cột trụ thường có hình dạng hình trụ. Tính toán thể tích giúp các kỹ sư dự đoán khả năng chịu lực và tải trọng của các công trình.

Trong Khoa Học

Trong các lĩnh vực như vật lý và hóa học, việc tính toán thể tích của hình trụ cũng rất quan trọng. Ví dụ, khi tiến hành thí nghiệm, nhà khoa học cần biết thể tích của các chất trong bình để chuẩn bị các mẫu thí nghiệm một cách chính xác.

4. Một Số Lưu Ý Khi Tính Thể Tích

Đơn Vị Đo Lường

Khi tính thể tích, cần chú ý đến các đơn vị đo lường. Thông thường, thể tích được đo bằng cm³, m³ hoặc lít. Hãy chắc chắn rằng bạn sử dụng đúng đơn vị để có kết quả chính xác.

Bán Kính và Chiều Cao

Khi đo bán kính và chiều cao, hãy đảm bảo rằng các phép đo được thực hiện chính xác. Một sai sót nhỏ trong việc đo đạc có thể dẫn đến sai số lớn trong thể tích tính toán.

Tính Đến Các Hình Khác

Ngoài hình trụ, còn nhiều hình dạng khác cũng có thể tính thể tích, như hình cầu, hình hộp chữ nhật hay hình nón. Mỗi hình dạng có một công thức riêng để tính thể tích. Việc so sánh thể tích các hình dạng này có thể giúp ích trong nhiều lĩnh vực khác nhau.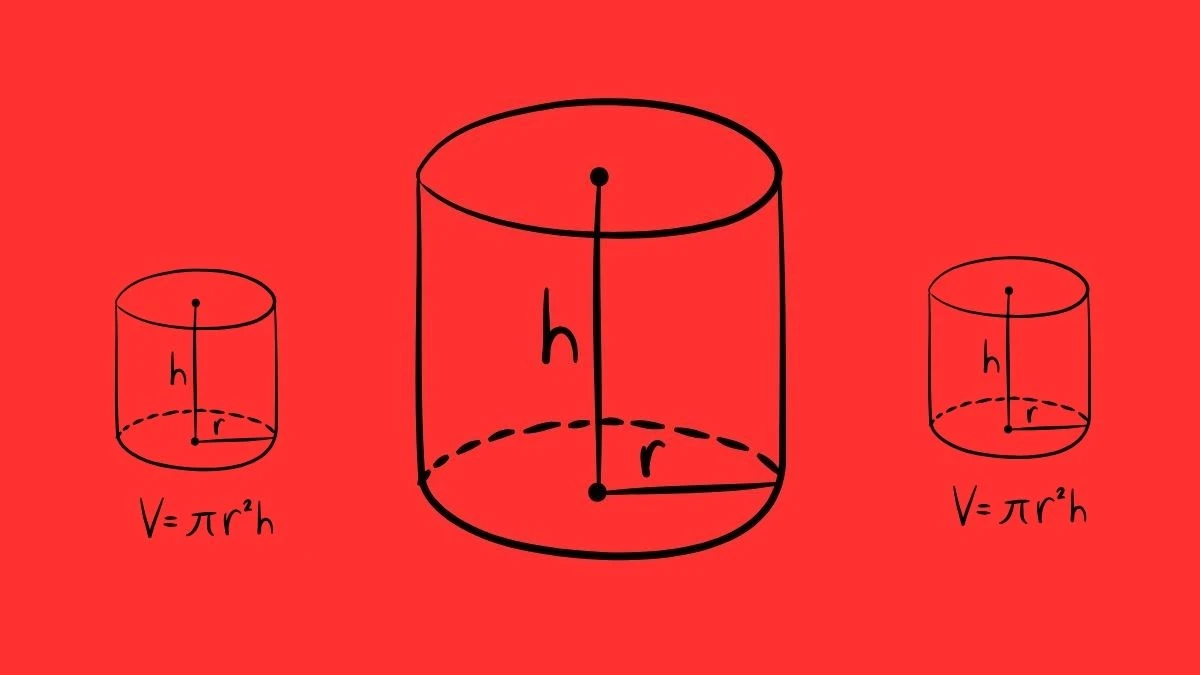

Kết Luận

Hình trụ là một trong những hình dạng cơ bản và quan trọng trong hình học. Việc hiểu và áp dụng công thức tính thể tích hình trụ không chỉ có giá trị trong học tập mà còn có nhiều ứng dụng trong thực tế. Bằng cách nắm vững lý thuyết và thực hành, bạn sẽ có thể giải quyết được nhiều bài toán hấp dẫn liên quan đến hình trụ và các hình dạng khác. Hy vọng bài viết đã giúp bạn có thêm kiến thức về thể tích của hình trụ và cách tính toán liên quan. Đừng ngần ngại thực hành để củng cố kiến thức của mình!